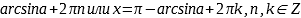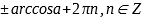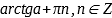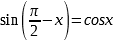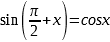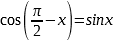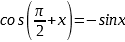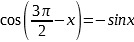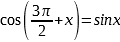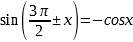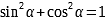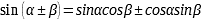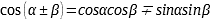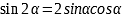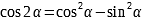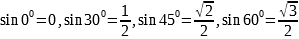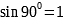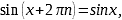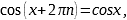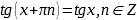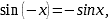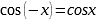Как решать задание 13 ЕГЭ по математике (профиль)
Учащиеся, приступающие к решению заданий повышенной сложности ЕГЭ 2024 г. по математике, чаще всего берутся за решение первого задания второй части, задания 13, из-за того, что оно проще остальных как по идейным соображениям, так и по техническому исполнению. Однако не всем удаётся избежать ошибок, а это влечёт снижение балла.
На реальных экзаменах последних лет в задании 13 требуется решить тригонометрическое уравнение и осуществить отбор корней, попадающих в заданный промежуток.
Критерии оценки результатов решения
Эксперт, проверяющий выполнение учащимся задание, выставляет баллы в строгом соответствии с критериями, приведёнными в таблице:
|
Содержание критерия |
Баллы |
|
Обоснованно получены верные ответы в обоих пунктах |
2 |
|
Обоснованно получен верный ответы в пункте а ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б |
1 |
|
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
|
Максимальный балл |
2 |
Обращаем внимание на то, что в критериях нет ни слова о способах решения задания. Это означает, что выбор способа решения и формы записи остаётся за учащимся, и не оценивается, оценивается математическая грамотность, обоснованность и полнота приведённого решения и ответа, а также отсутствие или наличие вычислительных ошибок.
Полнота и правильность приведённого решения и ответа определяются:
1. Выбором метода решения уравнения.
2. Соответствием выбранному методу верной последовательности всех необходимых шагов решения.
3. Обоснованием основных моментов решения уравнения и отбора корней.
4. Правильным применением формул, выполнением преобразований и вычислений.
5. Верным ответом и его соответствием условию задачи.
Что нужно знать для успешного решения задания 13.
|
Простейшие тригонометрические уравнения |
sinx=a
cosx=a
tgx=a |
|
Формулы приведения |
|
|
Тригонометрические формулы |
|
|
Табличные значения |
|
|
Свойства тригонометрических функций |
|
Разбор примеров решения задания 13 ЕГЭ по профильной математике
Пример 1.
а) Решите уравнение 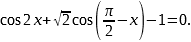
б) Укажите корни этого уравнения, принадлежащие отрезку 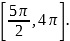
Решение.
а) Так как 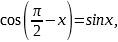 то преобразуем первое слагаемое следующим образом:
то преобразуем первое слагаемое следующим образом: 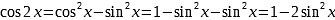 (конечно, можно сразу применить формулу понижения степени). Исходное уравнение примет вид
(конечно, можно сразу применить формулу понижения степени). Исходное уравнение примет вид
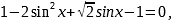
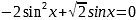 ,
, 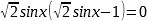 , откуда
, откуда
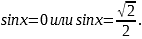
Если 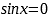 , то
, то 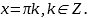
Если 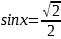 , то
, то 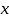 =
=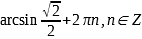 или
или 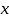 =
=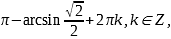 то есть
то есть 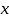 =
=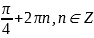 или
или 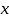 =
=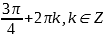
б) Произведём отбор корней уравнения, принадлежащих отрезку 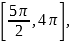 с помощью неравенств (можно осуществить отбор корней с помощью единичной окружности).
с помощью неравенств (можно осуществить отбор корней с помощью единичной окружности).
1. 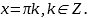
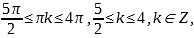 откуда k=3, k
=4.
откуда k=3, k
=4. 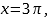
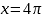 .
.
2. 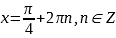 .
. 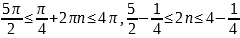 ,
, 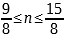 . Нет целых n, удовлетворяющих этому неравенству.
. Нет целых n, удовлетворяющих этому неравенству.
3. 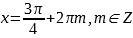
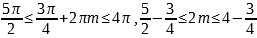 ,
, 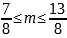 , m=1,
, m=1, 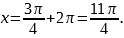
Корни уравнения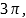
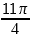 ,
, 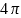 принадлежат отрезку
принадлежат отрезку 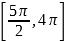 .
.
Ответ. а)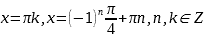 ; б)
; б) 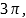
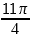 ,
, 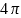 .
.
Обращаем внимание на то, что в критериях нет ни слова о способах решения задания. Это означает, что выбор способа решения и формы записи остаётся за учащимся, и не оценивается, оценивается математическая грамотность, обоснованность и полнота приведённого решения и ответа, а также отсутствие или наличие вычислительных ошибок.
Приведём пример решения задания 13 учащимся и комментарии эксперта.

Комментарий эксперта.
В пункте б) на тригонометрической окружности не установлено соответствие между обозначенными точками и найденными решениями (на окружности не отмечена точка 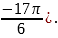 В соответствии с критериями оценивается в 1 балл.
В соответствии с критериями оценивается в 1 балл.
Пример 2.
а) Решите уравнение 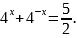
б) Найдите все корни этого уравнения, принадлежащие промежутку 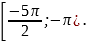
Решение. а) Обозначим 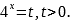 Уравнение примет вид t+
Уравнение примет вид t+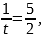
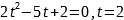 или
или 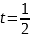 .
.
Вернёмся к исходной переменной.
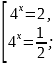
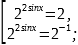
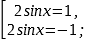
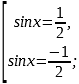
x=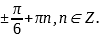
б) С помощью числовой окружности отберём корни, принадлежащие промежутку 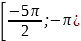 .
.
В указанном промежутке содержатся три корня
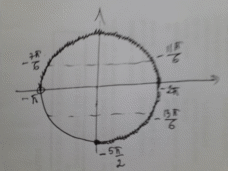
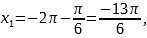
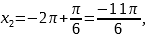

Ответ. а) x=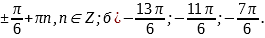
Похожие статьи
- Как решать задание 10 в ЕГЭ по математике (профиль)
- Как решать задание 15 в ЕГЭ по математике (профиль)
- Как решать задание 9 в ЕГЭ по математике (профиль)
- Как решать задание 18 в ЕГЭ по математике (профиль)